| End of year | $US in bank |
|---|---|
| 1 | $106.07 |
| 2 | $216.46 |
| 3 | $331.36 |
| 4 | $450.94 |
| 5 | $575.40 |
| 6 | $704.94 |
| 7 | $839.77 |
| 8 | $980.09 |
| 9 | $1,126.14 |
| 10 | $1,278.15 |
That's the argument, right? I spent $104 per year ($1040 total), and I only would have made $1278. Well, the right way to look at this is that you actually spent $1278, but that's beside the point. Yep, not a lot of money, and it probably wouldn't have made a big dent in your overall standard of living at the end of that 10 years...
But what about folks that spend $100 per week? Look at the numbers below!
| End of year | $US in bank |
|---|---|
| 1 | $5,303.32 |
| 2 | $10,822.99 |
| 3 | $16,567.83 |
| 4 | $22,547.03 |
| 5 | $28,770.15 |
| 6 | $35,247.14 |
| 7 | $41,988.36 |
| 8 | $49,004.59 |
| 9 | $56,307.04 |
| 10 | $63,907.39 |
That's $5,000 per year! At the end of 10 years, that's almost $64,000! So, go ahead and spend $2 per week on the lotto, but put the other $98 in the bank! (disclaimer: in a savings account that gives you 1/2% APR, the end amount is $53,000)
OK, got that out of my system. Playing the lottery is okay if you do it for fun - kind of like some people play bingo, etc., but don't do it with high hopes of striking it rich. It's better to stick the money in a savings account. It won't make as much as the megamillions payoff, but it'll probably make you more in the long run... (Oh, yeah... Whatever you win? Yeah, be prepared to pay nearly 70% of it to the man)
OK. now I've got it out of my system...
So, this gets me to thinking, though... Are there numbers that come up more often than others? Maybe the numbers are skewed, and if you figure out the patterns, maybe you can increase your odds? Now, I know that the lottery officials go through great pains to ensure the system is fair, that there is an equal likelihood that any of the balls will pop up on a given day. So, over a long number of draws, a histogram of all the numbers should look something like this:
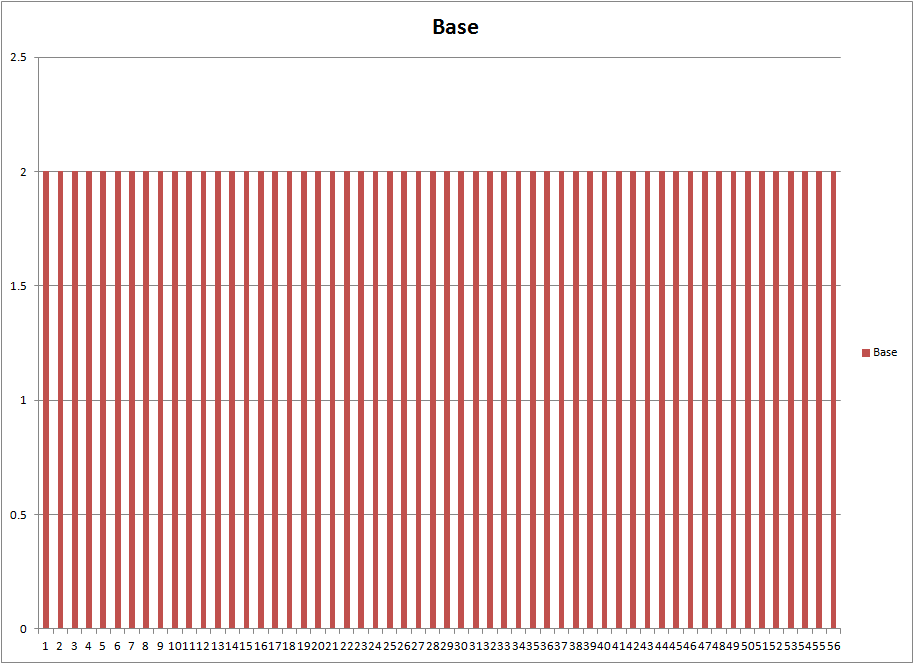
But what if the balls aren't perfect? Maybe big numbers have more drag (the larger numbers on the ball cause air flow from the machine to have a more pronounced effect, or something)? Or maybe something else is going on that has a similar overall effect, skewing the outcomes? That might be interesting to know. Maybe this is the reason why the lottery only keeps the last 25 draws?
*takes off tin foil hat*
It it also interesting to note that over a short period of time, you'll see certai numbers come up more often than others. This is called statistical clustering... This doesn't necessarily mean anything, just that those numbers came up a few times in a row. The graph below is for the 25 draws of the MegaMillions Lottery, up to January 1st, 2012:
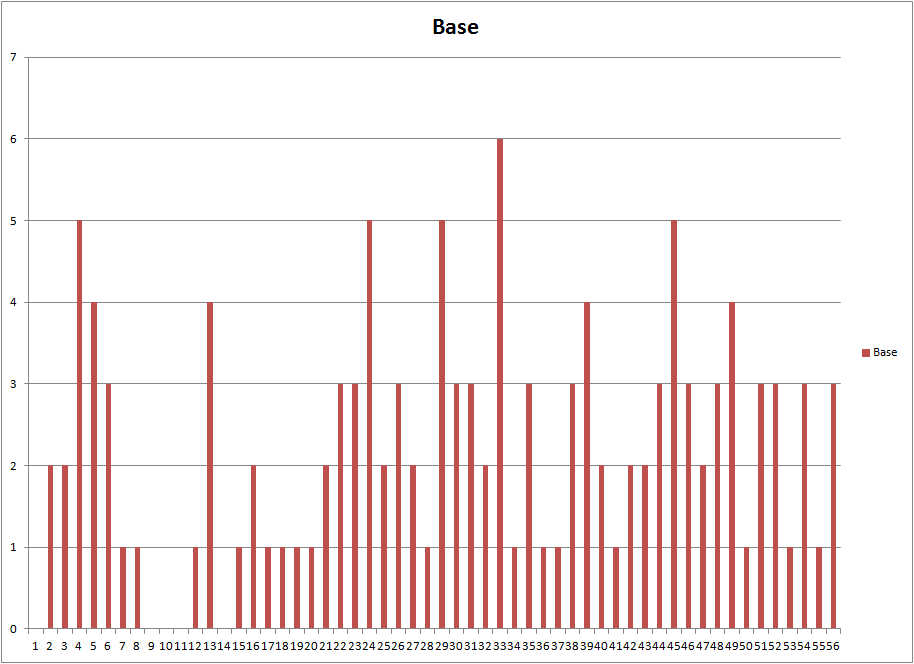
So, what does that mean? Well, see how 4, 24, 29, 32, and 45 came up more often than any others? Well, likely it means nothing, but maybe there's something up with hose balls? Conversely, if the histogram has to eventually become "flat" - well, then, at some point, those other numbers need to start coming up. So maybe the odds are better to choose the numbers that haven't come up? Or maybe it doesn't make a difference at all...
So, that's why this page is here. I'm doing a little private study to see what happens. Probably nothing. Yes, I'll play a couple bucks every week, too. I'll post my results as I see fit - that is, whenever I get around to it, if I remember. Maybe I'll figure out a way to automate all this, and then it won't be a big deal... Anyhoo, here's my picks for...
But first a disclaimer!
I make NO claim that anything I post here is worth anything to anybody. Period. Read this and spend your money at your own risk. If you have any sense, whatsoever, you'll put your money inthe bank, where at least you'll earn a little bit of interest. If you lose your ass, that's your own damned problem, capice?
That said, I also hold no obligation to anyone that happens to win using any number I might post here, either. Although, if you do win using one of my numbers, I wouldn't be heartbroken if you threw a little love my way, right?
Also, one last thing... I accept donations from anyone that would like to help me fund my bad habits. If you like what you see, feel free to send me a buck or two. Or ten. Or hundred. Heck, how 'bout a cool mil, in small, unmarked, non-consevutive bills?
So, here's my picks for the week of:
[an error occurred while processing this directive][an error occurred while processing this directive]
Last modified on 01/03/12